负载均衡算法之一 - 以 Golang 方式

题图：

load balancing diagram

FROM What Is Load Balancing? How Load Balancers Work

引子之前：

本来打算端午发的。无奈前几天实在是渴望休息放空脑子，就拖下来了。再一点是因为类库本身也没有时间去评估有没有什么忘记做的。

不过突然又觉得也无妨了，现在也就发了吧。

引子

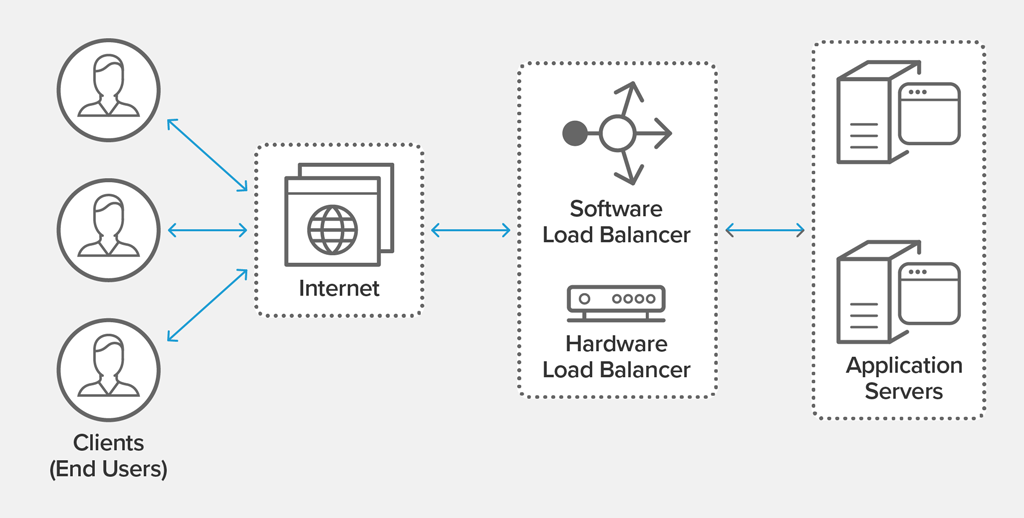
负载均衡被广泛运用在各种编排系统，微服务网关，Nginx/HAProxy 作为前置的网站集群等等场所。在看不到的更多领域，甚至于你所想象不到的，从未注意过的一些场所，负载均衡也以不同的面目在出没着，例如机械硬盘、硬盘组的读写访问，多核 CPU 的管线分配等等等等。

所以说负载均衡这种技术，以优化资源运用，最大化吞吐率，最小访问时延，防止过载为目标，存在着多种呈现方式。

由于负载均衡的基本特性在于调度输入到不同的计算单元，所以当某个计算单元失败时，负载均衡器能够选择正常工作的单元而避开该失败单元，当单元恢复正常工作时，负载均衡器也能正确地调度请求到该单元，这样的透明无感知的故障转移（failover）特性也往往被与负载平衡同时提及。例如公司的专线有三条，哪一条坏了无所谓，总还有好的线路让我们能够出口到云上去维护，这数条专线实际上就构成了能够故障转移的出口束。

在互联网中，最基础的服务，DNS 服务具有自动的负载均衡能力，只要你的域名有多个 A 记录来指示特定 IP 的服务器，那么这些服务器群就能够均匀地获取到输入请求并提供服务。

不过 DNS 服务在故障转移的特性上没有什么优势，所以限制了它可能的高级运用。正因为如此，我们所做的大型网站集群，前置部分一定是数台 nginx 所构成的前置代理器，在做了 DNS 负载均衡之后，仍需要冗余的再一层负载均衡器，因为这样才能将业务服务器群的变化（上下线）有效地掩盖起来。

除了采用 nginx/HAProxy 这类老牌的软件负载均衡工具之外，不差钱的公司也可以选用专用的硬件负载均衡器。

当视线收缩到业务服务器群上时，K8s 之类的编排软件主动提供了多种负载均衡形式来暴露它的私有网络中的节点和服务。

实际上 K8s 可能综合代价太大（额外的服务器和计算资源需求，额外的运维管理需求等），你们可能裸体就上云服务器了，无论是自研的服务治理还是采用知名框架例如 micro 或者 kong 之类的，它们也都提供了负载均衡调度能力。

抛开这些微服务架构不提，当你采用了融合到私有 DNS 服务器的 consul 集群时，这个小型的综合性 DNS 集群也能够提供增强的负载均衡能力，但可能需要一定的架构设计和相应的编码适配。

上面说了这么多，都不能掩盖一个论断：用软件实现负载均衡算法始终都有其存在的价值。因为当你的系统架构具备一定规模和复杂度之后，要求调度能力、要求摊薄请求时延、要求做到分治的 Map-Reduce 时，总之，你常常会需要手撸一小段负载均衡调度器，无论它可能会以怎样的面目出来。

所以，才有这组文章。

虽然已经有数不清的关于负载均衡的文章、论文、或者源码，但仍有这组文章，是因为它们都不是我的。我的，是我的。So，

基本的负载均衡算法

按照多方面综合来看，至少有这些最基本的负载均衡算法：

随机
轮询
最少连接数
hash
带权重的轮询

下面依次做一简单介绍，最后再来综述一遍。

前置的介绍

我总是喜欢编码，纯粹的编码。所以首先要介绍一些基本的接口设定：

type Peer interface {
	String() string
}

type Factor interface {
	Factor() string
}

type BalancerLite interface {
	Next(factor Factor) (next Peer, c Constrainable)
}

type Balancer interface {
  BalancerLite
  //...more
}

type FactorComparable interface {
	Factor
	ConstrainedBy(constraints interface{}) (peer Peer, c Constrainable, satisfied bool)
}

type FactorString string

func (s FactorString) Factor() string { return string(s) }

const DummyFactor FactorString = ""

type Constrainable interface {
	CanConstrain(o interface{}) (yes bool)
	Check(o interface{}) (satisfied bool)
	Peer
}

为了不必陷入设计细节，我提纲挈领地划重点做介绍：

Peer 是一个后端节点。
负载均衡器 Balancer 持有一组 Peers。
Factor 是 Balancer 在选取（Next(factor)）一个 Peer 时由调度者所提供的参考对象，Balancer 可能会将其作为选择算法工作的因素之一。
当你身为调度者时，想要调用 Next，却没有什么合适的“因素”提供的话，就提供 DummyFactor 好了。
Constrainable 在这组系列文章的最后时分可能会另行介绍，目前将其视而不见就足够了。

随机算法 Random

顾名思义，从后端列表中任意挑选一个出来，这就是随机算法。它最简单，结合我们的前置提示，请你综合理解下面的示例：

package main

import (
	"fmt"
	"github.com/hedzr/lb/lbapi"
	mrand "math/rand"
	"sync"
	"sync/atomic"
	"time"
)

type randomS struct {
	peers []lbapi.Peer
	count int64
}

func (s *randomS) Next(factor lbapi.Factor) (next lbapi.Peer, c lbapi.Constraintenable) {
	l := int64(len(s.peers))
	ni := atomic.AddInt64(&s.count, inRange(0, l)) % l
	next = s.peers[ni]
	return
}

func main() {
	lb := &randomS{
		peers: []lbapi.Peer{
			exP("172.16.0.7:3500"), exP("172.16.0.8:3500"), exP("172.16.0.9:3500"),
		},
		count: 0,
	}

	sum := make(map[lbapi.Peer]int)
	for i := 0; i < 300; i++ {
		p, _ := lb.Next(lbapi.DummyFactor)
		sum[p]++
	}

	for k, v := range sum {
		fmt.Printf("%v: %v\n", k, v)
	}
}

var seededRand = mrand.New(mrand.NewSource(time.Now().UnixNano()))
var seedmu sync.Mutex

func inRange(min, max int64) int64 {
	seedmu.Lock()
	defer seedmu.Unlock()
	return seededRand.Int63n(max-min) + min
}

type exP string

func (s exP) String() string { return string(s) }

randomS 实现了一个微型的、简单的随机算法的 LB。

尽管我也可以将其简化到只提供寥寥数行代码的片段，但是为了能够让它是 live & runnable 的，还是略微添加的 salt，示例由此而有点长，似乎不相干的东西也有一些。

运行结果可能是：

$ go run ./_examples/simple/random/
16.0.8:3500: 116
16.0.7:3500: 94
16.0.9:3500: 90

嗯，随机数发生器要均匀，数量级应该向 5K，乃至于 100K 的量级去才有意义。所以这里的结果并不是均分的，差不多也可以了。

正规化

需要提示的是，正式的 random LB 的代码要比上面的核心部分还复杂一点点。原因在于我们还需要达成另外两个设计目标：

线程安全
可嵌套

正因为 random LB 的关键算法只不过区区 3 行：

	l := int64(len(s.peers))
	ni := atomic.AddInt64(&s.count, inRange(0, l)) % l
	next = s.peers[ni]

所以我才有少少的篇幅来干脆提供正式版本的代码，其几乎完整的片段是这样：

package random

import (
	"github.com/hedzr/lb/lbapi"
	mrand "math/rand"
	"sync"
	"sync/atomic"
	"time"
)

var seededRand = mrand.New(mrand.NewSource(time.Now().UnixNano()))
var seedmu sync.Mutex

func inRange(min, max int64) int64 {
	seedmu.Lock()
	defer seedmu.Unlock()
	return seededRand.Int63n(max-min) + min
}

// New make a new load-balancer instance with Round-Robin
func New(opts ...lbapi.Opt) lbapi.Balancer {
	return (&randomS{}).init(opts...)
}

type randomS struct {
	peers []lbapi.Peer
	count int64
	rw    sync.RWMutex
}

func (s *randomS) init(opts ...lbapi.Opt) *randomS {
	for _, opt := range opts {
		opt(s)
	}
	return s
}

func (s *randomS) Next(factor lbapi.Factor) (next lbapi.Peer, c lbapi.Constraintenable) {
	next = s.miniNext()
	if fc, ok := factor.(lbapi.FactorComparable); ok {
		next, c, ok = fc.ConstraintBy(next)
	} else if nested, ok := next.(lbapi.BalancerLite); ok {
		next, c = nested.Next(factor)
	}
	return
}

func (s *randomS) miniNext() (next lbapi.Peer) {
	s.rw.RLock()
	defer s.rw.RUnlock()

	l := int64(len(s.peers))
	ni := atomic.AddInt64(&s.count, inRange(0, l)) % l
	next = s.peers[ni]
	return
}

func (s *randomS) Count() int {
	s.rw.RLock()
	defer s.rw.RUnlock()
	return len(s.peers)
}

func (s *randomS) Add(peers ...lbapi.Peer) {
	for _, p := range peers {
		s.AddOne(p)
	}
}

func (s *randomS) AddOne(peer lbapi.Peer) {
	if s.find(peer) {
		return
	}

	s.rw.Lock()
	defer s.rw.Unlock()
	s.peers = append(s.peers, peer)
}

func (s *randomS) find(peer lbapi.Peer) (found bool) {
	s.rw.RLock()
	defer s.rw.RUnlock()
	for _, p := range s.peers {
		if lbapi.DeepEqual(p, peer) {
			return true
		}
	}
	return
}

func (s *randomS) Remove(peer lbapi.Peer) {
	s.rw.Lock()
	defer s.rw.Unlock()
	for i, p := range s.peers {
		if lbapi.DeepEqual(p, peer) {
			s.peers = append(s.peers[0:i], s.peers[i+1:]...)
			return
		}
	}
}

func (s *randomS) Clear() {
	s.rw.Lock()
	defer s.rw.Unlock()
	s.peers = nil
}

对比前后两者，应该能够展示出 #%$&#%@ 的代码竟然有辣么多，:)

仅此一次，下面都不会有了。

轮询算法 Round-Robin

你其实可能并不知道 robin 究竟是谁。

它其实是谁都不是，最早它是一个法语词汇 ruban，意思是丝带缎带 Ribbon。但是时间冲刷了一切，后来不知道怎么滴，就以讹传讹渐渐演变成 robin 了。

The term round-robin is derived from the French term ruban, meaning “ribbon”. Over a long period of time, the term was corrupted and idiomized to robin.

—— Round-robin tournament

源于循环赛制的 round and ruban，最后也就称为了 Round-robin。至于中文版 Wiki 所提到的 round-robin letter，也不妨去看一看。当然，至于是不是爱安门的 Robin，那就是纯粹的休闲时间了。

好的，这些根本不重要。重要的是这个轮询算法就是挨个选择一个 peer。就是这样。

所以它的算法核心大体上是这样子的：

func (s *rrS) miniNext() (next lbapi.Peer) {
	ni := atomic.AddInt64(&s.count, 1)
	ni %= int64(len(s.peers))
	next = s.peers[ni]
	return
}

s.count 会一直增量上去，并不会取模，这样做的用意在于如果 peers 数组发生了少量的增减变化时，最终发生选择时可能会更模棱两可。

对于 Golang 来说，s.count 来到 int64.MaxValue 时继续加一会自动回绕到 0。这一特性和多数主流编译型语言相同，都是 CPU 所提供的基本特性。

最少连接数 Least Connections

如果一个后端服务上的活动都连接数时全部后端中最少的，那么就选它了。

这个算法不给实例了，因为很多时候管理活动连接数是个不寻常的内务，麻烦不小，也会消耗额外的资源——这个资源可不是做作加法或者取个模——所以除了像 nginx 之类的专业代理服务器之外实际上用得到它的不多。

只要你的系统能够很恰当地管理自己的后端的连接数，实作一份 Least Connections LB 没有什么算法上的疑难问题。

Hashing 以及 Consistent Hashing

回顾

在早些年，没有区分微服务和单体应用的那些年，Hash 算法的负载均衡常常被当作神器，因为 session 保持经常是一个服务无法横向增长的关键因素，而针对用户的 session-id 的 hash 值进行调度分配时，就能保证同样 session-id 的来源用户的 session 总是落到某一确定的后端服务器，从而确保了其 session 总是有效的。

在 Hash 算法被扩展之后，很明显，可以用客户端 IP 值，主机名，url 或者无论什么你想得到的东西去做 hash 计算，只要得到了 hashCode，就可以应用 Hash 算法了。而像诸如客户端 IP，客户端主机名之类的标识由于其相同的 hashCode 的原因，所以对应的后端 peer 也能保持一致，这就是 session 年代 hash 算法显得重要的原因。

越明年，政通人和，都不用 browser session 方式了，取而代之的是无状态模型，所以 hash 算法其实有点落寞了。

无状态模型的本质是在 header 中带上 token，这个 token 将能够被展开为用户身份登录后的标识，从而等效于 browser session。说了个半天，无状态模型，例如 JWT 等，其原始的意图就是为了横向缩放服务器群。

稍后，1997 年 MIT 的 Karger 发表了所谓一致性 Hashing 的算法论文，其与传统的 hashCode 计算的关键性不同在于，一方面将 hashCode 约束为一个正整数（int32/uint32/int64 等等），一方面将正整数空间 [0, int.MaxValue] 视为一个可回绕的环形，即所谓的 Hash Ring，而待选择的 peers 均匀地分布在这个环形上，从而保证了每次选取时能够充分平滑地选取到每个 peer。

至于选取时的下标值的计算方面是没有限定的，所以你可以在这个下标值的计算方案上加入可选策略。

在负载均衡领域中的一致性 Hash 算法，又加入了 Replica 因子，它实际上就是在计算 Peer 的 hash 值时为 peer 的主机名增加一个索引号的后缀，索引号增量 replica 次，这样就得到了该 peer 的 replica 个副本。这就将原本 n 台 peers 的规模扩展为 n x Replica 的规模，有助于进一步提高选取时的平滑度。

代码实现

所以说了这么多，其算法核心大致是这样的：

type Hasher func(data []byte) uint32

// hashS is a impl with ketama consist hash algor
type hashS struct {
	hasher   Hasher // default is crc32.ChecksumIEEE
	replica  int    // default is 32
	hashRing []uint32
	keys     map[uint32]lbapi.Peer
	peers    map[lbapi.Peer]bool
	rw       sync.RWMutex
}

func (s *hashS) Next(factor lbapi.Factor) (next lbapi.Peer, c lbapi.Constraintenable) {
	var hash uint32
	hash = s.hasher([]byte(factor.Factor()))

	ix := sort.Search(len(s.hashRing), func(i int) bool {
		return s.hashRing[i] >= hash
	})

	if ix == len(s.hashRing) {
		ix = 0
	}

	hashValue := s.hashRing[ix]
	if p, ok := s.keys[hashValue]; ok {
		if _, ok = s.peers[p]; ok {
			next = p
		}
	}

	return
}

func (s *hashS) Add(peers ...lbapi.Peer) {
	for _, p := range peers {
		s.peers[p] = true
		for i := 0; i < s.replica; i++ {
			hash := s.hasher(s.peerToBinaryID(p, i))
			s.hashRing = append(s.hashRing, hash)
			s.keys[hash] = p
		}
	}

	sort.Slice(s.hashRing, func(i, j int) bool {
		return s.hashRing[i] < s.hashRing[j]
	})
}

func (s *hashS) peerToBinaryID(p lbapi.Peer, replica int) []byte {
	str := fmt.Sprintf("%v-%05d", p, replica)
	return []byte(str)
}

在 Add 实现中建立了 hashRing 结构，它虽然是环形，但是是以数组和下标取模的方式来达成的。此外，keys 这个 map 解决从 peer 的 hash 值到 peer 的映射关系，今后（在 Next 中）就可以通过从 hashRing 上 pick 出一个 point 之后立即地获得相应的 peer.

在 Next 中主要是在做 factor 的 hash 值计算，计算的结果在 hashRing 上映射为一个点 pt，如果不是恰好有一个 peer 被命中的话，就向后扫描离 pt 最近的 peer。

算法思想扼要扫尾

其实不打算写这一段了，因为别人家画的图真好看啊，讲的也透彻。

譬如说这张图：

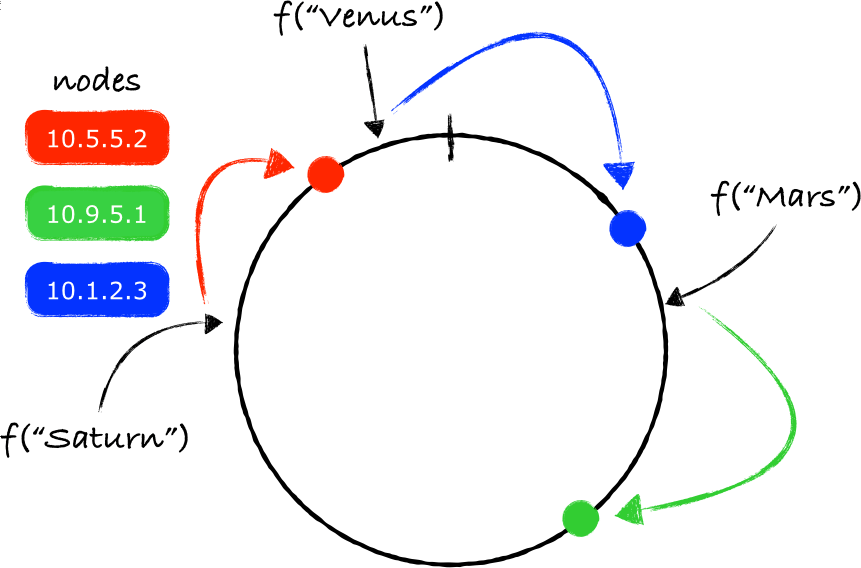
FROM Wayne’s Blog - System Design 101 - Consistent Hashing

keynote，流口水啊，我真的打算去学学了。

你要是对这个算法的每一细节都感兴趣的话，还可以看看这两个视频：

前面我们提到了 replica，它是在 hashRing 上创建 peers 的虚拟节点的一种方法，这种思路是为了尽可能提高 peers 发生变化后导致的不均匀不平滑的选择结果问题。基本上最早其来自于 libketama，一个 memcached 库，所以多数情况下同样的思路被称作 Ketama Hashing 算法。可以参考这里。

带权重的轮询算法 Weighted Round-robin

加上权重，是一个很重要的特性。所以在基本的 LB 算法章节我们需要以加权轮询（wrr）为例来提到它。

加权轮询算法，是给每个 peer 增加一个权重，在平均化轮询的基础上加上这个权重来作为调节。

最著名的加权轮询算法实现要论及 Nginx 和 LVS 了。

Nginx 平滑加权轮询

Nginx 采用一种依据 total 和各个权重之间的差值来平衡选择的方法：每次选择时，都对每个节点的 currentWeight 加上其权重值，然后选择 currentWeight 最大的那个节点，同时该节点的 currentWeight 在减去其权重值复原到增量前。如此反复选择之下，权重大的节点由于增量速度更快而被选中的更多。

这一算法思想可以得到严格的数学证明，不过我就不说这一块了，要点是核心实现：

func (s *wrrS) Next() (best lbapi.Peer) {
	total := 0
	for _, node := range s.peers {
		if node == nil {
			continue
		}

		total += s.mUpdate(node, 0, false)
		if s.mTest(best, node) {
			best = node
		}
	}

	if best != nil {
		s.mUpdate(best, -total, true)
	}
	return
}

func (s *wrrS) mUpdate(node lbapi.Peer, delta int, success bool) (total int) {
	if delta == 0 {
		delta = s.m[node].weight
	}
	s.m[node].current += delta
	return s.m[node].weight
}

func (s *wrrS) mTest(best, node lbapi.Peer) bool {
	return best == nil || s.m[node].current > s.m[best].current
}

上述代码做了提炼，实际上的代码还要复杂一些，因为我们还需要做锁操作。

LVS 平滑加权轮询

至于 LVS 的加权轮询法，核心思想在于采用 gcd（最大公约数）的方式。

/*
 Supposing that there is a server set S = {S0, S1, …, Sn-1};
 W(Si) indicates the weight of Si;
 i indicates the server selected last time, and i is initialized with -1;
 cw is the current weight in scheduling, and cw is initialized with zero; 
 max(S) is the maximum weight of all the servers in S;
 gcd(S) is the greatest common divisor of all server weights in S;
*/
while (true) {
    i = (i + 1) mod n;
    if (i == 0) {
        cw = cw - gcd(S); 
        if (cw <= 0) {
            cw = max(S);
            if (cw == 0)
            return NULL;
        }
    } 
    if (W(Si) >= cw) 
        return Si;
}

你可以这样来理解它：对于三个节点 A，B，C，权重为 x,y,z 时，想象有一个数组，其中填充了 x 次 A，y 次 B，z 次 C，然后用轮询法扫描这个数组，是不是最终的选中比例就满足权重分配了？

实际上，很多年前，我的第一份 wrr 实现就是这么弄的，后来遇到权重值很大，然后就很烦恼，直到后来某一天我看到 LVS 算法的介绍，才感叹真的就是本啊。

小结

上面已经解说了主要的基本 LB 算法。

这几种基本算法还可以进一步组合演变，例如

加权随机算法
（请求）来源 Hash
目的地 Hash
加权最少连接数算法
等等

我们想要在新的类库中达成这些目的，所以需要进一步的代码设计和重组。篇幅原因，下一次我们再来阐述做一个类库会需要些什么样的思考。

Twitter Facebook LinkedIn

负载均衡算法之一 - 以 Golang 方式

hedzr

引子

基本的负载均衡算法

前置的介绍

随机算法 Random

正规化

轮询算法 Round-Robin

最少连接数 Least Connections

Hashing 以及 Consistent Hashing

回顾

代码实现

算法思想扼要扫尾

带权重的轮询算法 Weighted Round-robin

Nginx 平滑加权轮询

LVS 平滑加权轮询

小结

分享

留下评论

猜您还喜欢

关于 std:barrier

Git Tips - 怎么才能在 git log 之后保留屏幕输出

go.work 在开源库开发中的运用

使用 CMake Presets