谈 C++17 里的 State 模式之一

介绍 fsm-cxx 的实现

回顾状态模式，考虑实作它的各种问题——特别是有关如何实现一个状态机的问题。同时，这一篇呢，可能不得不分几篇，因为写的时候脑壳在发散嘛，于是就关联得到的、能想起来的都提了一嘴，就多了。但是最后还是会给出代码的，我喜欢写代码的。

注：

文中不会做固定式理论介绍（像通常的 Design Patterns 书籍那样的固定版式），你需要相关背景知识的初步了解；有深入了解更好，有助于相互印证。

但是你也可以全无了解，藉此入门后再进入教科书。为此我也努力约束术语的精确使用，尽力不带来误解。

本文应该是无趣的，我只是在整理。

Prologue

状态模式，是指一个对象 A 拥有多种不同的状态，当特定条件满足时，对象 A 由一种状态切换到另一种，且在不同状态时（可能）具有不同的外在表现。据此，对象 A 将总是有一个开始状态 S，当状态正在发生转换时，我们说前一状态为当前状态 C，而将要转换到的状态为下一状态 N。而当状态转换完成时，当前状态也就切换到了下一状态。

如果有必要，状态模式可能存在着一个终止状态 T。对于一段输入序列来说，如果输入终了，可能会触发到迁移到终止状态；或者特定的标记（Token）会做出这样的触发，例如 Pascal 语言翻译机在遇到 END. 标记时就结束一个编译单元的编译处理。

从广义上讲，状态模式和状态机、编译器有着密切乃至于等价的关系。你可以把状态模式视为简版的编译器，这算是一种约定俗成的习语。而多数语境里，大家对状态模式和状态机不作区分，但有的时候，如果我们的讨论语境较为学术性时，那么多半会采用状态机这一术语。

2021-09-07 23:35

State Pattern

理论

状态模式是一种结构型的设计模式，它往往和状态机、有限状态机、自动机、编译原理、UML 状态图等近似或关联性概念一起被混用以及同时提起。

一般来说，我们认为状态模式就是状态机的一种实现范式。因此本文中会将状态模式与如何实现一个状态机等同起来。

提到状态机，它首先表示的是一个对象拥有一系列状态，并且能够在状态之间相互状态，而当发生转换时则会触发特定的动作 Action（分为进入动作 Entry Action 和退出动作 Exit Action，以及输入动作 Input Action，有时候也包括转移动作 Transition Action），并表现出不同的外在形象。

分类

状态机/自动机（Automaton）可以被分为多种类别：

1. 接受器/识别器/序列检测器，Acceptors - 例如 gcc 这样的编译器接受一个正规文法序列，正确完成编译的序列则被认为是可接受的。
2. 变换器，Transducers - 重点在于给定输入可以引发动作，生成输出。这一类状态机还可以细分为两个小类：Moore Machine 和 Mealy Machine。

除了上述的主要划分之外，还有其它分类方式。

例如分类器 Classfiers 和序列（时序/音序等）测定器/生成器 Sequencers。将多个接受器按照确定性与否，则可划分为 DFA 与 NFA 等。在确定型自动机（DFA）中，每个状态对每个可能输入只有精确的一个转移。在非确定型自动机（NFA）中，给定状态对给定可能输入可以没有或有多于一个转移。

等等。

Moore Machine

Moore Machine 的特点是只使用进入动作，就是说输出只依赖于当前状态，与输入信号（如果有）无关。

例如电梯门的运行到站和超时时开闭的状态图：

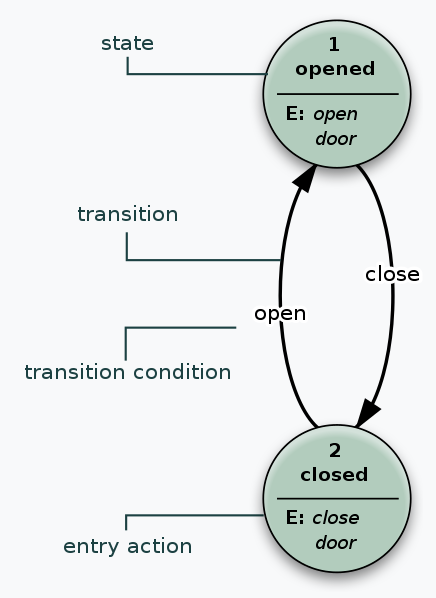
图示中，从状态 Opened 只能迁移到 Closed，当进入到 Opened 时其进入动作 open door 会导致电机启动并开门，而从状态 Closed 也只能迁移到 Opened，其进入动作 close door 导致电机反向启动并关门。

图示中没有绘制的是外界反应或者内部反应，例如开门时间超时状态机推进到关门状态、或者电梯运行到楼层导致推进到开门状态，但我们考察的只是一个子系统，从而得以演示出摩尔机的概念。如果我们用不同的其它尺度来观察电梯门系统，则可能产生其他结果。

由上例可见，Moore 机的状态转换只依赖于当前状态，只使用进入动作，相对来说是很简单的。

对于 Moore 机来说，状态转换需要一个推动力，这是通常的状态机教材没有显示提及的。通常状态机不可能自行驱动自身从一个状态变迁到另一状态，所以它需要一个驱动力。在上例电梯门的 Moore 机中，Somebody 按下开门关门钮就是这个驱动信号。

Mealy Machine

Mealy Machine 的状态切换依赖于输入动作以及当前状态，它比摩尔机更复杂一点，但同时也常常因此而使得其状态图更简单简约。例如电梯门被开闭的状态图：

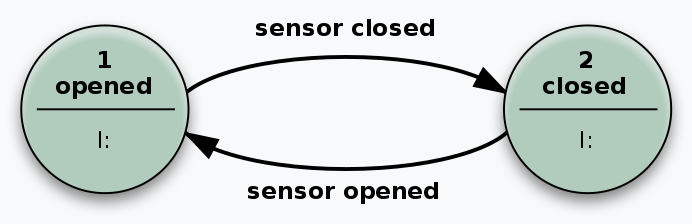
图示中，由于开门按钮按下（sensor opened）导致电梯门从 closed 状态切换到 opened，由于关门按钮按下（sensor closed）导致反向转换。

和摩尔机的示例有所不同，这个例子中视角聚焦在电梯门是如何受到传感器信号的触发而改变的。

同样的道理，这个例子也有驱动信号的存在：尽管同样是开门关门按钮按下导致门开门关，但驱动信号在这个例子中是门开门关传感器所产生的信号，传感器检测到门开门关动作后发出信号，以标示电梯门进入到新的状态（门已开，门已关）。所以同一个事件，精细考察不同的局部，会得到不同的结论。

TCP 的状态跃迁图

TCP 的状态跃迁图能够很好地展示状态的切换：

FROM: PDF - TCP/IP State Transition Diagram (RFC793)

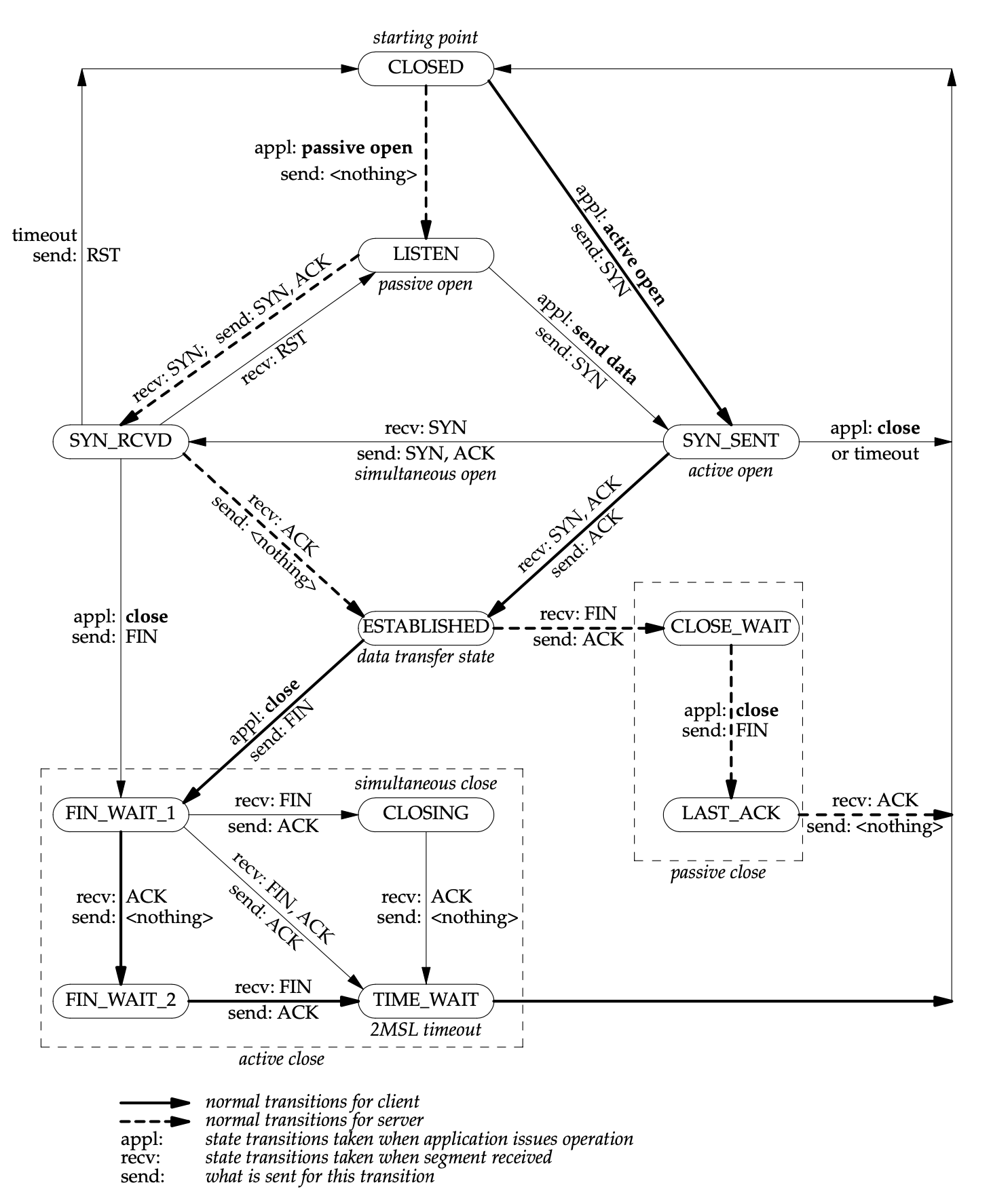
为了帮助不熟悉的朋友多角度观察，这里也提供另一张图可供相互佐证：

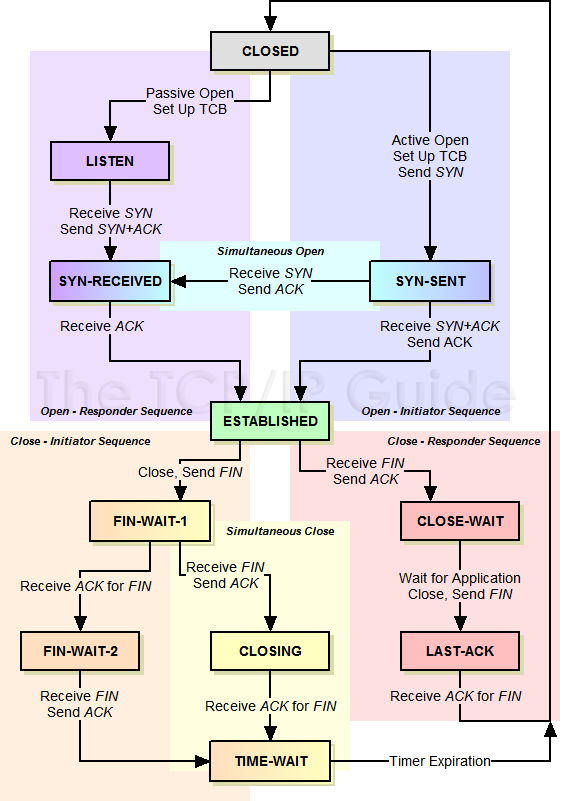
FROM: The TCP/IP Guide - TCP Operational Overview and the TCP Finite State Machine (FSM)

实现方法介绍

可以有几种方式来实现一个状态机/状态模式（可以被称作自动机编程范式）：

1. 完全手写条件和转换
2. 查表法
3. DFA 技术

实现状态模式最直觉的方法，是采用一系列的 if..else 或者 switch 语句，但这种方式在状态较多，转换路径复杂时将会很被动。一个简短的例子如下：

#include <stdio.h>
enum states { before, inside, after };
void step(enum states *state, int c) {
  if(c == '\n') {
    putchar('\n');
    *state = before;
  } else
    switch(*state) {
      case before:
        if(c != ' ') {
          putchar(c);
          *state = inside;
        }
        break;
      case inside:
        if(c == ' ') {
          *state = after;
        } else {
          putchar(c);
        }
        break;
      case after:
        break;
    }
}

int main(void) {
  int c;
  enum states state = before;
  while((c = getchar()) != EOF) {
    step(&state, c);
  }
  return 0;
}

所以一般来说的正确实现方式是利用一张二维的转换表，通过查表的方式求得下一状态从而完成转换。而开发者首先要做的就是分析需求并编制出这么一张转换表再说。

另外，在 C++ metaprogramming 世界里，通常就不会使用一张明确的转换表了，替代这张表的手段是利用 hash_map 的方式建立从状态 from 到 to 的转换关系。这种方式在我们后边的具体实现中会有一个展示。但是它仍然是一种查表法。

稍后再粗略谈论 FSM（编译原理中的 FSM）和 DFA 技术的实现概要。

查表法

状态机的转换规则可以表示为一张二维的状态转移表，像这样：

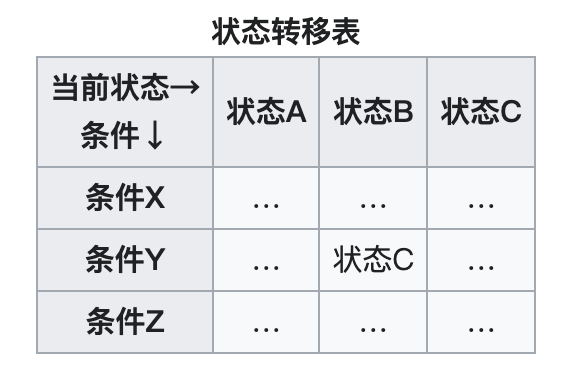
在实际场景中，这张表往往是比较稀疏的，很多交叉点是没有到下一状态的跃迁可能性的，所以这张表所映射到的二维数组通常都可以采取一定的措施以将其压缩下来，压缩的结果除了能显著降低表的存储空间之外，也有可能明显地降低扫描这张表的速度。

对于无需参考输入条件的 Moore 机来说，没有纵向的条件表，替代它的是一个单调的信号，该信号促使状态机发生步进动作，因此条件表依然是有效的。

FSM，NFA 和 DFA

真正实用的状态模式实现手段，都是采用查表法的。

如果不是，那么它们采用的是查表法的某种形式的变体。

在将理论进一步深入之后，状态模式可以上升到有限状态机（FSM，Finite-State Machine） 的高度，在这一层次研究相同的状态机问题时，我们将会采用在编译原理中必备的基础研究方式。

面对一台 FSM，我们首先是罗列并绘制出状态变迁图，然后通过技术手段（典型地如 Thompsion 构造法）将文法描述转换为 NFA（Nondeterministic Finite Automaton，非确定性有限状态机），然后借助于经过了严格证明的理论将 NFA 转换为 DFA（Deterministic Finite Automaton，确定性有限状态机）。值得一提的是，NFA 到 DFA 的转换也是个刻板无趣的过程，并且往往会导致新增大量的中间性过渡型状态，所以 DFA 可能比 NFA 大很多倍。一个 DFA 的数据结构表示，通常是一张巨大的、经过了规约之后的二维数组（等效于前面所描述的二维的转换表），面对输入的字符集，在这个转换表中能够直接求得下一状态。同时，这张表中的空洞也很多，这是因为从一个状态到另一个状态的变迁关系当然不会是笛卡尔积的，所以说它总是会是一张稀疏的二维数组。

言归正传，经过一系列的正规文法上的约束和求解之后，我们总是能够从正规文法的描述上获得对应的转换表，这是经由了数学证明后的结论。最终，我们（通常、经常）需要压缩标准的 DFA，将其所占据的庞大的空间进行收缩，但功用不变，就形成了最后的 FSM 工作机。

上述的过程可以提炼为：

1. 绘制状态变迁图
2. 计算 NFA
3. 转换为 DFA
4. 压缩 DFA
5. 配套一个查表算法的代码

一般地，在编译器领域，完成上面一系列操作的东西叫做编译器的编译器，这会使用术语 LEX 来简称，由于近代以来基本上是 Flexible LEX 一家独大，所以我们常常也称之为 FLEX（这是Unix/Linux 系统上的一个软件，事实上的编译器领域的准则和标准）。而由 LEX 所创建出来的则是编译器（等效于 gcc），而编译器则被看作是能够吃进一段符合某种文法的源代码的机器，这台机器解释源代码的词法和语法为机器码，每当吃进一个 token 时，编译器就推动内部状态从前一状态迁移到下一状态，同时做出一定的反应（处理某些 action）。

当然，实用的多数编译器的 FSM 部分，也即编程语言的文法翻译部分，除了理论研究时采用 Flex & Bison（也即 LEX & YACC）之外，现实实现中往往采用手写来完成，原因在于手写版本可以糅合编码人的脑力规约，常常在特定形态的翻译时显著地缩减编译的资源需求，这是面对现实世界时的一种妥协与选择，不提。

如果对有限状态机以及 NFA -> DFA 感兴趣，请阅读编译原理的经典教材。

所谓非确定性有限状态机 NFA/NDFA，是指给定状态对于给定输入可以有任意多个转移（0..N）。此时若要想正确完成转换，可能需要向后继续预察看和预匹配才能一次性地连续转进多个状态。

而确定性有限状态机 DFA的每个状态对于每个可能的输入有且只有一个精确的转移。

可见对于 CPU 运算来讲我们最终需要一个 DFA 模型才能有效运转，而 NFA 则会导致我们的处理逻辑过分复杂（look-ahead）甚至于完全无法实现。学术研究在上世纪5、60年代就已经确定了任何正规文法的 NFA 均能够被转换为等价的 DFA（代价是更多更复杂的中间状态，参考 Kleene 闭包）。

因此才会有 LEX（一种 Unix 软件）工具的出现。

这种实现方式非常正统与学院派，但是由于它与编译原理的联系如此紧密，因此通常在非编译器实现的其它领域中，我们总是称呼自动机为状态机，并且实现方式更多地倾向于不采用 DFA 手法。

这只是通常情况，没有人能阻止你用牛刀杀鸡。

另外转头思考，DFA 技法实际上隐含着一个前提，它的事件激励是通过流式输入的元素序列来达到的，所以对于编译器来说吃进字符序列是个顺理成章的机制，而在这个领域中也发展了正规文法以及正则式等一系列关联性理论，它们之间都是相辅相成的。而 DFA 技法被应用在其它场合中时就有点麻烦、或者说不合理了。尽管我们还是可以将事件信号采用某种方式流化（例如一连串的鼠标事件以及键盘事件被串行化后通过消息泵传送到分发器时，分发器也可以构造一个 DFA 形式的表格来完成状态迁移、顺便再触发相关的 action，也没什么不可以），但这就不一定是实作时的最佳选择了：所以 UI 消息分发器通常还是采用动作函数的到事件发生器（sender）的绑定方式，这样做有利于代码维护和相关逻辑的维护，若是用一张 DFA 表呢，这个维护就很艰难了。

OK，在本文中，我们采用 FSM 术语来暗指 FSM 以及 NFA 以及 DFA 等一系列特有的技术概念与实现，并隐含着它们将在编译原理的上下文中被提及。此外我们将其它情况中的状态模式称为实现一个状态机。

但是在其它文章中，FSM 可能仅仅只是包含状态机而不必上升到 DFA 计算层次。

进一步的分类

在经典的状态机理论之上，UML 规范提供了增强的状态机算法模型。相比较而言，UML 状态机（绘制成 UML 图时就叫做 state chart）的增强之处在于：

1. HFSM，Hierarchy FSM，即所谓层级状态机、分层状态机、嵌套状态机。中文叫法多样，但却是同一个东西，也就是说在大的状态机里某个状态包含了一组成系列的子级状态机。

   举个例子，计算器具有开、关状态，而开机后的计算机又有输入状态、求值状态、连续求值状态等等一系列子状态。

   

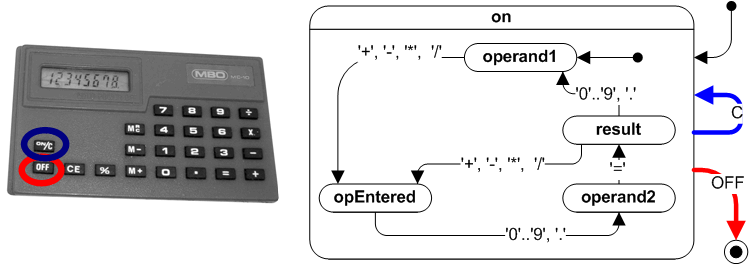
   https://en.wikipedia.org/wiki/UML_state_machine#/media/File:UML_state_machine_Fig2b.png

2. 正交区域 Orthogonal regions

3. 等等

HFSM 在游戏开发领域中、芯片设计、FPGA 设计、PLC 设计等场所里非常常见。

有时候我们也可以将普通的状态机进行抽象后构成更细腻的分区，从而得到 HFSM 的形态，例如编译器在解释可嵌套的注释块时，实际上就进入了子状态机的工作模态，但有别于正规的 HFSM 处理流程的是，编译器对于子状态往往是直白地用额外的代码（action）对其予以解决，并不将其流程化、或者表格化。

谈到 HFSM 时常常又会同时提到另一个概念：行为树（Behavior Tree）。行为树这种东西并不是一个良好的算法表述（在一棵树上遍历节点时、节点的特性完全不同），它实际上是给人看的，是一种 HFSM 的图解方式。换句话说，行为树的随意性较高，没有良好的约束条件，所以需要管理者付出额外力量来保证不会产生冲突和竞争（例如在不同节点层次结构中的 actions 中）。

如果想更多了解 HFSM 以及 BT，可以看看：

PDF - HFSM & BT - stanford cs123

游戏业中喜欢讲行为树我的实现多么有特点，多么 AI，是的，从不同的角度完成 FSM 是非常有价值的，它使得状态迁移的规则更易于被管理，不过这玩意和 AI 还是搭不上界的。

小小结

一般来说，我们认为状态模式就是状态机的一种实现范式。因此本文中会将状态模式与如何实现一个状态机等同起来。

由于在计算机科学中我们总是研究状态数规模具有上限的状态机，所以我们所实现的状态机也将总会是一种有限状态机（FSM）。FSM 通常与编译原理紧密结合。

无论如何，还是要总结一下：

状态模式通常可以被看作为 FSM 的轻量级版本。这是因为常常我们会认为少量状态的变迁可以直接手写（包括手工构造状态转换表），不必引入严格的理论求证作为依据。而一旦状态变迁规模变大，或者工程需求提出了严格的目标要求时，那么我们就应该采用 FSM 方式（DFA方式）来确保编码实现的冥等性。

像 TCP 的状态变迁，规模不大，完全可以手写，除非你希望做严格的理论推导或者学术研究，否则泰半无需兴师动众。但是对于现代化的 RegExp 进行翻译和解释，手写通常行不通（也不绝对，确实曾有团队是硬撸的），只能借助于 Kleene 闭包的手段完成到 DFA 的翻译后完成构造，而那是非常省力的。

下一部分

只能留待下一篇再来谈论具体的实现案例了。

Epilogue

未完待续。